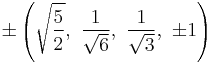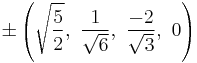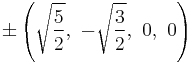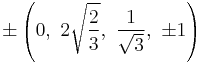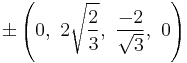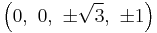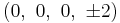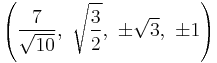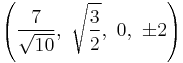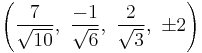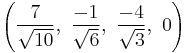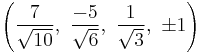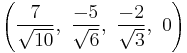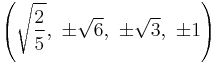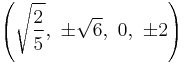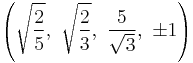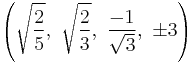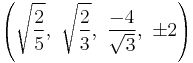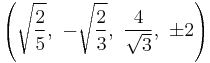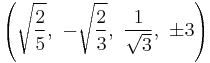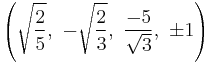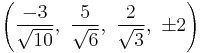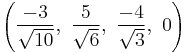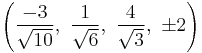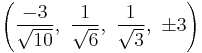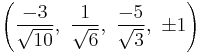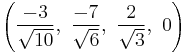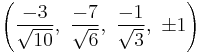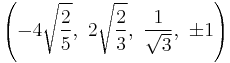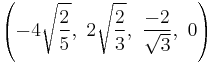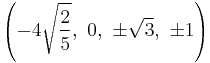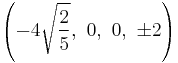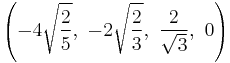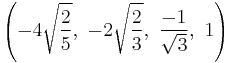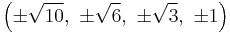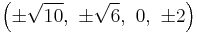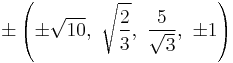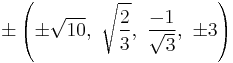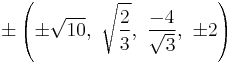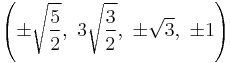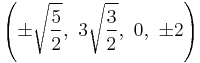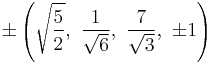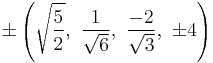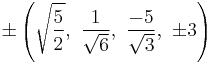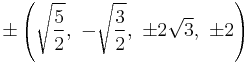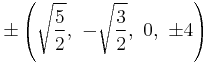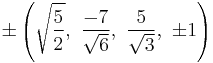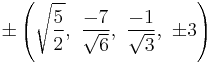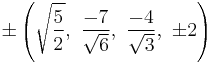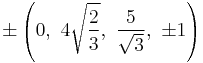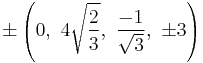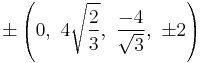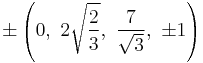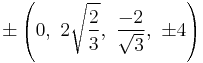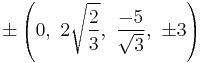Runcinated 5-cell

Orthogonal projections in A₄ Coxeter plane
5-cell	Runcinated 5-cell
Runcitruncated 5-cell	Omnitruncated 5-cell (Runcicantitruncated 5-cell)

In four-dimensional geometry, a runcinated 5-cell is a convex uniform polychoron, being a runcination (a 3rd order truncation) of the regular 5-cell.

There are 3 unique degrees of runcinations of the 5-cell including with permutations truncations and cantellations.

Runcinated 5-cell

Runcinated 5-cell
Schlegel diagram with half of the tetrahedral cells visible.
Type	Uniform polychoron
Schläfli symbol	t_0,3{3,3,3}
Coxeter-Dynkin diagram
Cells	30	10 (3.3.3) 20 (3.4.4)
Faces	70	40 {3} 30 {4}
Edges	60
Vertices	20
Vertex figure	(Elongated equilateral-triangular antiprism)
Symmetry group	[[3,3,3]], order 240
Properties	convex, isogonal isotoxal
Uniform index	4 5 6

The runcinated 5-cell is constructed by expanding the cells of a 5-cell radially and filling in the gaps with triangular prisms (which are the face prisms and edge figures) and tetrahedra (cells of the dual pentachoron). It consists of 10 tetrahedra and 20 triangular prisms. The 10 tetrahedra correspond with the cells of a 5-cell and its dual.

Alternative names

Runcinated 5-cell (Norman Johnson)
Runcinated pentachoron
Runcinated 4-simplex
Expanded 5-cell/4-simplex/pentachoron
Small prismatodecachoron (Acronym: Spid) (Jonathan Bowers)

Root vectors

Its 20 vertices represent the root vectors of the simple Lie group A₄. It is also the vertex figure for the 5-simplex honeycomb in 4-space.

Structure

Two of the ten tetrahedral cells meet at each vertex. The triangular prisms lie between them, joined to them by their triangular faces and to each other by their square faces. Each triangular prism is joined to its neighbouring triangular prisms in anti orientation (i.e., if edges A and B in the shared square face are joined to the triangular faces of one prism, then it is the other two edges that are joined to the triangular faces of the other prism); thus each pair of adjacent prisms, if rotated into the same hyperplane, would form a gyrobifastigium.

Images

orthographic projections
A_k Coxeter plane	A₄	A₃	A₂
Graph
Dihedral symmetry	[[5]]=[10]	[4]	[[3]]=[6]

View inside of a 3-sphere projection Schlegel diagram with its 10 tetrahedral cells

Coordinates

The Cartesian coordinates of the vertices of an origin-centered runcinated 5-cell with edge length 2 are:

$\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{1}{\sqrt{3}},\ \pm1\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{-2}{\sqrt{3}},\ 0\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ -\sqrt{\frac{3}{2}},\ 0,\ 0\right)$	$\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{1}{\sqrt{3}},\ \pm1\right)$ $\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{-2}{\sqrt{3}},\ 0\right)$ $\left(0,\ 0,\ \pm\sqrt{3},\ \pm1\right)$ $\left(0,\ 0,\ 0,\ \pm2\right)$

An alternate simpler set of coordinates can be made in 5-space, as 20 permutations of:

(0,1,1,1,2)

This construction exists as one of 32 orthant facets of the runcinated 5-orthoplex.

Cross-sections

The maximal cross-section of the runcinated 5-cell with a 3-dimensional hyperplane is a cuboctahedron. This cross-section divides the runcinated 5-cell into two tetrahedral hypercupolas consisting of 5 tetrahedra and 10 triangular prisms each.

Projections

The tetrahedron-first orthographic projection of the runcinated 5-cell into 3-dimensional space has a cuboctahedral envelope. The structure of this projection is as follows:

The cuboctahedral envelope is divided internally as follows:

Four flattened tetrahedra join 4 of the triangular faces of the cuboctahedron to a central tetrahedron. These are the images of 5 of the tetrahedral cells.
The 6 square faces of the cuboctahedron are joined to the edges of the central tetrahedron via distorted triangular prisms. These are the images of 6 of the triangular prism cells.
The other 4 triangular faces are joined to the central tetrahedron via 4 triangular prisms (distorted by projection). These are the images of another 4 of the triangular prism cells.
This accounts for half of the runcinated 5-cell (5 tetrahedra and 10 triangular prisms), which may be thought of as the 'northern hemisphere'.

The other half, the 'southern hemisphere', corresponds to an isomorphic division of the cuboctahedron in dual orientation, in which the central tetrahedron is dual to the one in the first half. The triangular faces of the cuboctahedron join the triangular prisms in one hemisphere to the flattened tetrahedra in the other hemisphere, and vice versa. Thus, the southern hemisphere contains another 5 tetrahedra and another 10 triangular prisms, making the total of 10 tetrahedra and 20 triangular prisms.

Related skew polyhedron

The regular skew polyhedron, {4,6|3}, exists in 4-space with 6 squares around each vertex, in a zig-zagging nonplanar vertex figure. These square faces can be seen on the runcinated 5-cell, using all 60 edges and 20 vertices. The 40 triangular faces of the runcinated 5-cell can be seen as removed. The dual regular skew polyhedron, {6,4|3}, is similarly related to the hexagonal faces of the bitruncated 5-cell.

Runcitruncated 5-cell

Runcitruncated 5-cell
Schlegel diagram with cuboctahedral cells shown
Type	Uniform polychoron
Schläfli symbol	t_0,1,3{3,3,3}
Coxeter-Dynkin diagram
Cells	30	5 (3.6.6) 10 (4.4.6) 10 (3.4.4) 5 (3.4.3.4)
Faces	120	40 {3} 60 {4} 20 {6}
Edges	150
Vertices	60
Vertex figure	(Rectangular pyramid)
Coxeter group	A₄, [3,3,3], order 120
Properties	convex, isogonal
Uniform index	7 8 9

The runcitruncated 5-cell is composed of 60 vertices, 150 edges, 120 faces, and 30 cells. The cells are: 5 truncated tetrahedra, 10 hexagonal prisms, 10 triangular prisms, and 5 cuboctahedra. Each vertex is surrounded by five cells: one truncated tetrahedron, two hexagonal prisms, one triangular prism, and one cuboctahedron; the vertex figure is a rectangular pyramid.

Alternative names

Runcitruncated pentachoron
Runcitruncated 4-simplex
Diprismatodispentachoron
Prismatorhombated pentachoron (Acronym: prip) (Jonathan Bowers)

Images

orthographic projections
A_k Coxeter plane	A₄	A₃	A₂
Graph
Dihedral symmetry	[5]	[4]	[3]

Schlegel diagram with its 40 blue triangular faces and its 60 green quad faces.	Central part of Schlegel diagram.

Coordinates

The Cartesian coordinates of an origin-centered runcitruncated 5-cell having edge length 2 are:

$\left(\frac{7}{\sqrt{10}},\ \sqrt{\frac{3}{2}},\ \pm\sqrt{3},\ \pm1\right)$ $\left(\frac{7}{\sqrt{10}},\ \sqrt{\frac{3}{2}},\ 0,\ \pm2\right)$ $\left(\frac{7}{\sqrt{10}},\ \frac{-1}{\sqrt{6}},\ \frac{2}{\sqrt{3}},\ \pm2\right)$ $\left(\frac{7}{\sqrt{10}},\ \frac{-1}{\sqrt{6}},\ \frac{-4}{\sqrt{3}},\ 0\right)$ $\left(\frac{7}{\sqrt{10}},\ \frac{-5}{\sqrt{6}},\ \frac{1}{\sqrt{3}},\ \pm1\right)$ $\left(\frac{7}{\sqrt{10}},\ \frac{-5}{\sqrt{6}},\ \frac{-2}{\sqrt{3}},\ 0\right)$ $\left(\sqrt{\frac{2}{5}},\ \pm\sqrt{6},\ \pm\sqrt{3},\ \pm1\right)$ $\left(\sqrt{\frac{2}{5}},\ \pm\sqrt{6},\ 0,\ \pm2\right)$ $\left(\sqrt{\frac{2}{5}},\ \sqrt{\frac{2}{3}},\ \frac{5}{\sqrt{3}},\ \pm1\right)$	$\left(\sqrt{\frac{2}{5}},\ \sqrt{\frac{2}{3}},\ \frac{-1}{\sqrt{3}},\ \pm3\right)$ $\left(\sqrt{\frac{2}{5}},\ \sqrt{\frac{2}{3}},\ \frac{-4}{\sqrt{3}},\ \pm2\right)$ $\left(\sqrt{\frac{2}{5}},\ -\sqrt{\frac{2}{3}},\ \frac{4}{\sqrt{3}},\ \pm2\right)$ $\left(\sqrt{\frac{2}{5}},\ -\sqrt{\frac{2}{3}},\ \frac{1}{\sqrt{3}},\ \pm3\right)$ $\left(\sqrt{\frac{2}{5}},\ -\sqrt{\frac{2}{3}},\ \frac{-5}{\sqrt{3}},\ \pm1\right)$ $\left(\frac{-3}{\sqrt{10}},\ \frac{5}{\sqrt{6}},\ \frac{2}{\sqrt{3}},\ \pm2\right)$ $\left(\frac{-3}{\sqrt{10}},\ \frac{5}{\sqrt{6}},\ \frac{-4}{\sqrt{3}},\ 0\right)$ $\left(\frac{-3}{\sqrt{10}},\ \frac{1}{\sqrt{6}},\ \frac{4}{\sqrt{3}},\ \pm2\right)$ $\left(\frac{-3}{\sqrt{10}},\ \frac{1}{\sqrt{6}},\ \frac{1}{\sqrt{3}},\ \pm3\right)$	$\left(\frac{-3}{\sqrt{10}},\ \frac{1}{\sqrt{6}},\ \frac{-5}{\sqrt{3}},\ \pm1\right)$ $\left(\frac{-3}{\sqrt{10}},\ \frac{-7}{\sqrt{6}},\ \frac{2}{\sqrt{3}},\ 0\right)$ $\left(\frac{-3}{\sqrt{10}},\ \frac{-7}{\sqrt{6}},\ \frac{-1}{\sqrt{3}},\ \pm1\right)$ $\left(-4\sqrt{\frac{2}{5}},\ 2\sqrt{\frac{2}{3}},\ \frac{1}{\sqrt{3}},\ \pm1\right)$ $\left(-4\sqrt{\frac{2}{5}},\ 2\sqrt{\frac{2}{3}},\ \frac{-2}{\sqrt{3}},\ 0\right)$ $\left(-4\sqrt{\frac{2}{5}},\ 0,\ \pm\sqrt{3},\ \pm1\right)$ $\left(-4\sqrt{\frac{2}{5}},\ 0,\ 0,\ \pm2\right)$ $\left(-4\sqrt{\frac{2}{5}},\ -2\sqrt{\frac{2}{3}},\ \frac{2}{\sqrt{3}},\ 0\right)$ $\left(-4\sqrt{\frac{2}{5}},\ -2\sqrt{\frac{2}{3}},\ \frac{-1}{\sqrt{3}},\ 1\right)$

The vertices can be more simply constructed on a hyperplane in 5-space, as the permutations of:

(0,1,1,2,3)

This construction is from the positive orthant facet of the runcitruncated 5-orthoplex.

Omnitruncated 5-cell

Omnitruncated 5-cell
Schlegel diagram with half of the truncated octahedral cells shown.
Type	Uniform polychoron
Schläfli symbol	t_0,1,2,3{3,3,3}
Coxeter-Dynkin diagram
Cells	30	10 (4.6.6) 20 (4.4.6)
Faces	150	90{4} 60{6}
Edges	240
Vertices	120
Vertex figure	(Chiral irregular tetrahedron)
Coxeter group	A₄, [[3,3,3]], order 240
Properties	convex, isogonal, zonotope
Uniform index	8 9 10

The omnitruncated 5-cell is composed of 120 vertices, 240 edges, 150 faces (90 squares and 60 hexagons), and 30 cells. The cells are: 10 truncated octahedra, and 20 hexagonal prisms. Each vertex is surrounded by four cells: two truncated octahedra, and two hexagonal prisms, arranged in two chiral irregular tetrahedral vertex figures.

Coxeter calls this Hinton's polytope after C. H. Hinton, who described it in his book The Fourth Dimension in 1906. It forms a uniform honeycomb which Coxeter calls Hinton's honeycomb.^[1]

Alternative names

Omnitruncated 5-cell
Omnitruncated pentachoron
Omnitruncated 4-simplex
Great prismatodecachoron (Acronym: gippid) (Jonathan Bowers)
Hinton's polytope (Coxeter)

Images

orthographic projections
A_k Coxeter plane	A₄	A₃	A₂
Graph
Dihedral symmetry	[[5]]=[10]	[4]	[[3]]=[6]

Perspective projections

Perspective Schlegel diagram Centered on truncated octahedron	Stereographic projection

Permutohedron

Just as the truncated octahedron is the permutohedron of order 4, the omnitruncated 5-cell is the permutohedron of order 5.^[2] The omnitruncated 5-cell is a zonotope, the Minkowski sum of five line segments parallel to the five lines through the origin and the five vertices of the 5-cell.

Orthogonal projection as a permutohedron

Tessellations

The omnitruncated 5-cell honeycomb can tessellate 4-dimensional space by translational copies of this cell, each with 3 hypercells around each face. This honeycomb's Coxeter-Dynkin diagram is .^[3] Unlike the analogous honeycomb in three dimensions, the bitruncated cubic honeycomb which has three different Coxeter group Wythoff constructions, this honeycomb has only one such construction.^[1]

Coordinates

The Cartesian coordinates of the vertices of an origin-centered omnitruncated 5-cell having edge length 2 are:

$\left(\pm\sqrt{10},\ \pm\sqrt{6},\ \pm\sqrt{3},\ \pm1\right)$ $\left(\pm\sqrt{10},\ \pm\sqrt{6},\ 0,\ \pm2\right)$ $\pm\left(\pm\sqrt{10},\ \sqrt{\frac{2}{3}},\ \frac{5}{\sqrt{3}},\ \pm1\right)$ $\pm\left(\pm\sqrt{10},\ \sqrt{\frac{2}{3}},\ \frac{-1}{\sqrt{3}},\ \pm3\right)$ $\pm\left(\pm\sqrt{10},\ \sqrt{\frac{2}{3}},\ \frac{-4}{\sqrt{3}},\ \pm2\right)$ $\left(\pm\sqrt{\frac{5}{2}},\ 3\sqrt{\frac{3}{2}},\ \pm\sqrt{3},\ \pm1\right)$ $\left(\pm\sqrt{\frac{5}{2}},\ 3\sqrt{\frac{3}{2}},\ 0,\ \pm2\right)$	$\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{7}{\sqrt{3}},\ \pm1\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{-2}{\sqrt{3}},\ \pm4\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{-5}{\sqrt{3}},\ \pm3\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ -\sqrt{\frac{3}{2}},\ \pm2\sqrt{3},\ \pm2\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ -\sqrt{\frac{3}{2}},\ 0,\ \pm4\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ \frac{-7}{\sqrt{6}},\ \frac{5}{\sqrt{3}},\ \pm1\right)$ $\pm\left(\sqrt{\frac{5}{2}},\ \frac{-7}{\sqrt{6}},\ \frac{-1}{\sqrt{3}},\ \pm3\right)$	$\pm\left(\sqrt{\frac{5}{2}},\ \frac{-7}{\sqrt{6}},\ \frac{-4}{\sqrt{3}},\ \pm2\right)$ $\pm\left(0,\ 4\sqrt{\frac{2}{3}},\ \frac{5}{\sqrt{3}},\ \pm1\right)$ $\pm\left(0,\ 4\sqrt{\frac{2}{3}},\ \frac{-1}{\sqrt{3}},\ \pm3\right)$ $\pm\left(0,\ 4\sqrt{\frac{2}{3}},\ \frac{-4}{\sqrt{3}},\ \pm2\right)$ $\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{7}{\sqrt{3}},\ \pm1\right)$ $\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{-2}{\sqrt{3}},\ \pm4\right)$ $\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{-5}{\sqrt{3}},\ \pm3\right)$

These vertices can be more simply obtained in 5-space as the 120 permutations of (0,1,2,3,4). This construction is from the positive orthant facet of the runcicantitruncated 5-orthoplex, t_0,1,2,3{3,3,3,4}, .

Related polytopes

These polytopes are a part of a family of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol	{3,3,3}	t_0,1{3,3,3}	t₁{3,3,3}	t_0,2{3,3,3}	t_1,2{3,3,3}	t_0,1,2{3,3,3}	t_0,3{3,3,3}	t_0,1,3{3,3,3}	t_0,1,2,3{3,3,3}
Coxeter-Dynkin diagram
Schlegel diagram
A₄ Coxeter plane Graph
A₃ Coxeter plane Graph
A₂ Coxeter plane Graph

Notes

^ ^a ^b The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (The classification of Zonohededra, page 73
^ The permutahedron of order 5
^ George Olshevsky, Uniform Panoploid Tetracombs, manuscript (2006): Lists the tessellation as [140 of 143] Great-prismatodecachoric tetracomb (Omnitruncated pentachoric 4d honeycomb)

References

H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
1. Convex uniform polychora based on the pentachoron – Model 5, 8, and 9, George Olshevsky.
Richard Klitzing, 4D, uniform polytopes (polychora) o3x3x3o - spid, x3x3o3x - prip, x3x3x3x - gippid


Family	A_n	BC_n	D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square		Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
n-polytopes	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes

Runcinated 5-cell

Contents